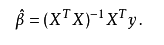Raymond Yang

Introduction

Linear analytics is a human instinct way predict result based on limited training data. Linear Regression is the process to come out a linear model. This post will dive deeper into the mathematics conclude procedure of Linear regression.

Simple Linear Regression

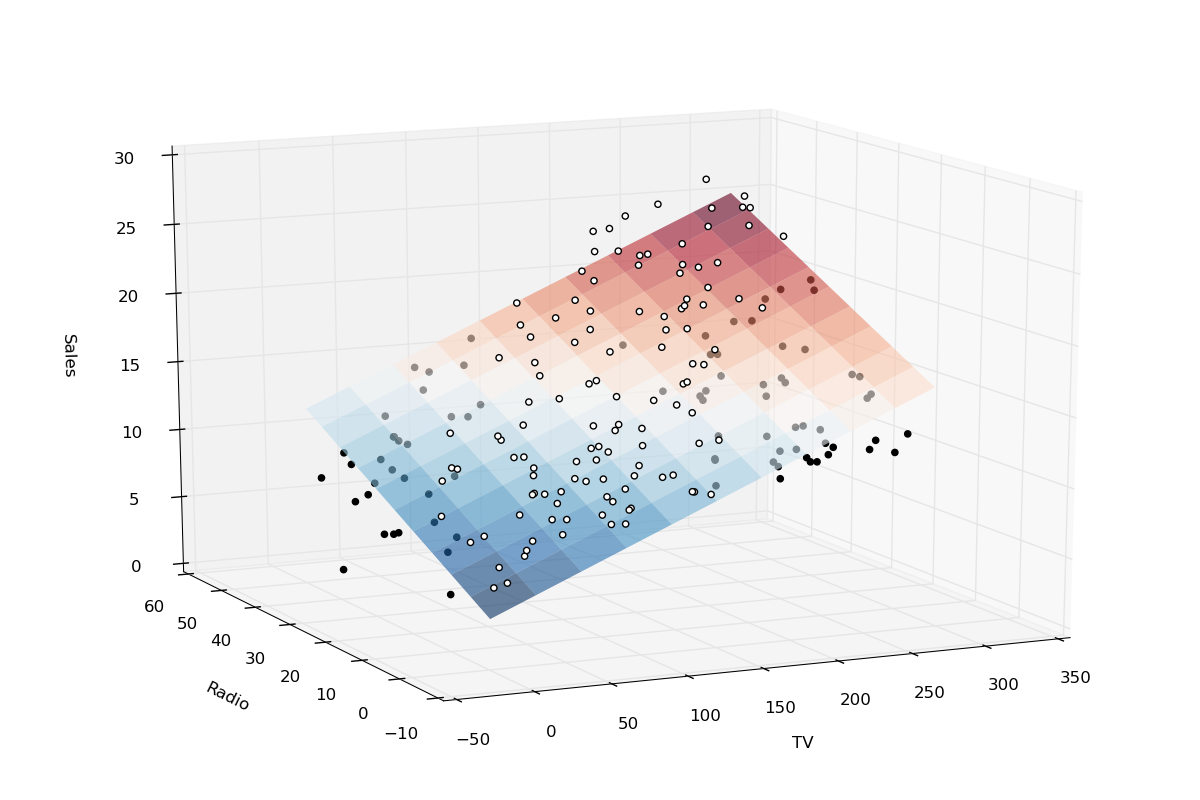
Starting from the simple linear regression. The training data is 2-dimension. x is the input data and y is the expected result. It allows us to draw a linear function in a 2-dimension coordinate system.

To find the best model, we’re looking for a model with least square.

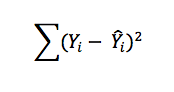
By expanding the least square equation, we will get a quadratic equation contians variable k and b as below.

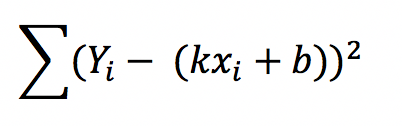
Now, to solve this equation, I’m going to calculate the partial derivative to k and b. Because we know that a quadratic equation must have its maximum or minimum value. In this equation, it has minimum value. By solving the partial derivative equations, we can know the corresponding value for k and b when the quadratic equation getting its minimum value.

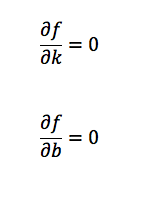
Expand the equation and we get

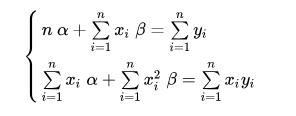
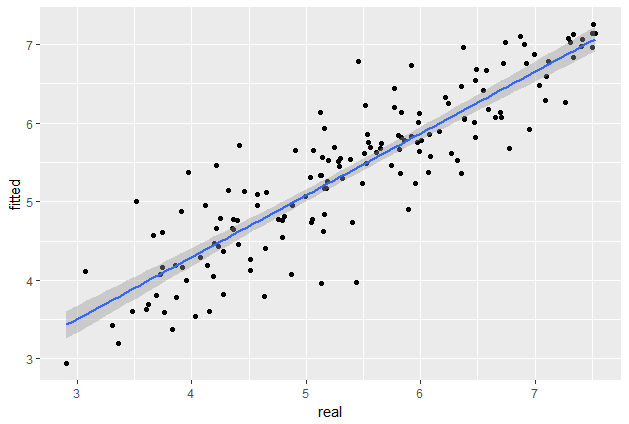
Solve this equation set and we finally get

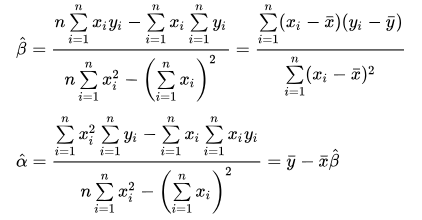
Now we can calculate the best model for simple linear regression.

Multi dimension Linear Regression

For multi-dimension input, the mathematics idea is same, which is using ordinary least square method. This time, instead of having 2 equations in the set, we calculate the partial derivative for each cofficient.

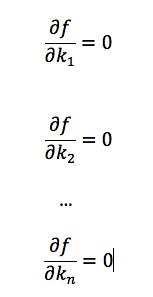
We will get n + 1 equations in the set and we can use the same steps to calculate the cofficient for the best model.